Maze
Feel free to take a tour, but good luck finding your way out of this one!
To start with we have a stripped binary and a server running that binary; we get the flag if we make it validate.
❯ ./maze_public
Please type your input:
hi
Try again!
Looks like we're trying to find the input which makes it not say "Try again!"? Let's open it up and see how it makes that decision!
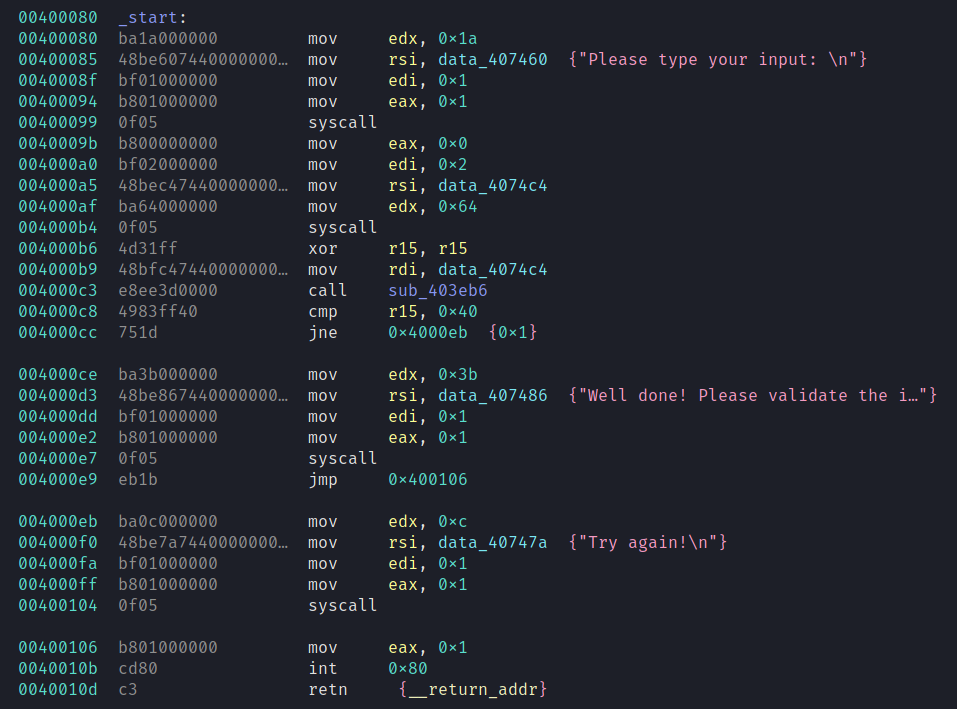
Ah syscalls, lovely -- we read in some input and pass it to sub_403eb6. If the return value is 64 we get the flag.
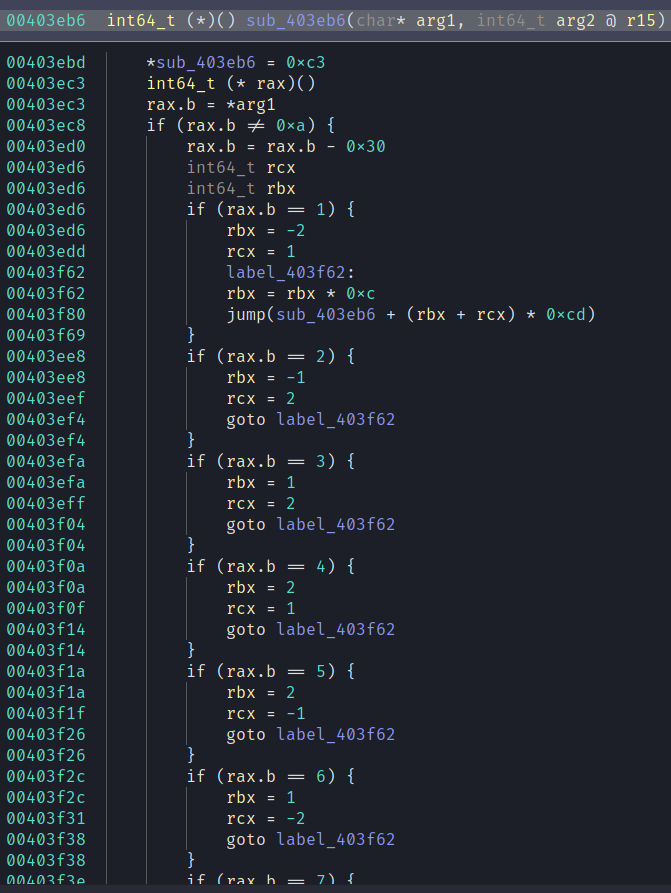
This is real gnarly. You can't see the bottom of the function in that picture but here is a summary.
- Set the first byte to 0xc3 (ret in x86)
- You can't see it in the decompilation but it increments the register r15 (this is used as a return value when the function returns)
- Retrieve the first byte of the input and increment the pointer (so the next function will get the next byte)
- Set rbx and rcx based on the byte (only accepts 1-8)
- Jumps to one of 8 successor functions based on rbx and rcx; some of these successor functions will immediately return
So immediately we're looking to do a graph traversal of this to find a path of 64 functions. My first attempt involved patching the binary to write r15 to stdout and then writing a naive depth first traversal based on inputs which increase the depth. Unfortunately this turned out to be super not tractable; I came back an hour later to 57-58 length paths and it had spent most of the hour around that same length.
As it turns out there are only 64 unique nodes which makes this problem significantly harder. We're looking to find a hamiltonian path which for a directed cyclic graph (this unfortunately has many cycles) is NP-complete and a naive solution will finish approximately fucking never. Fortunately there are heuristic solutions which can be applied to solve it in a reasonable amount of time.
lifting it into a graph
This ended up actually being really straightforward! The "directions" aka values of rbx & rcx are constant which means we have two values to extract for each function -- the address of the function and the address it uses as a base to compute successor functions.
405ebe: 48 8d 05 f9 ff ff ff lea rax,[rip+0xfffffffffffffff9] # 0x405ebe
405ec5: c6 00 c3 mov BYTE PTR [rax],0xc3
405ec8: 49 ff c7 inc r15
405ecb: 8a 07 mov al,BYTE PTR [rdi]
405ecd: 48 ff c7 inc rdi
405ed0: 3c 0a cmp al,0xa
405ed2: 0f 84 b2 00 00 00 je 0x405f8a
405ed8: 2c 30 sub al,0x30
405eda: 3c 01 cmp al,0x1
405edc: 75 0e jne 0x405eec
405ede: 48 c7 c3 fe ff ff ff mov rbx,0xfffffffffffffffe
405ee5: b9 01 00 00 00 mov ecx,0x1
405eea: eb 7e jmp 0x405f6a
405eec: 3c 02 cmp al,0x2
405eee: 75 0e jne 0x405efe
405ef0: 48 c7 c3 ff ff ff ff mov rbx,0xffffffffffffffff
405ef7: b9 02 00 00 00 mov ecx,0x2
405efc: eb 6c jmp 0x405f6a
405efe: 3c 03 cmp al,0x3
405f00: 75 0c jne 0x405f0e
405f02: bb 01 00 00 00 mov ebx,0x1
405f07: b9 02 00 00 00 mov ecx,0x2
405f0c: eb 5c jmp 0x405f6a
405f0e: 3c 04 cmp al,0x4
405f10: 75 0c jne 0x405f1e
405f12: bb 02 00 00 00 mov ebx,0x2
405f17: b9 01 00 00 00 mov ecx,0x1
405f1c: eb 4c jmp 0x405f6a
405f1e: 3c 05 cmp al,0x5
405f20: 75 0e jne 0x405f30
405f22: bb 02 00 00 00 mov ebx,0x2
405f27: 48 c7 c1 ff ff ff ff mov rcx,0xffffffffffffffff
405f2e: eb 3a jmp 0x405f6a
405f30: 3c 06 cmp al,0x6
405f32: 75 0e jne 0x405f42
405f34: bb 01 00 00 00 mov ebx,0x1
405f39: 48 c7 c1 fe ff ff ff mov rcx,0xfffffffffffffffe
405f40: eb 28 jmp 0x405f6a
405f42: 3c 07 cmp al,0x7
405f44: 75 10 jne 0x405f56
405f46: 48 c7 c3 ff ff ff ff mov rbx,0xffffffffffffffff
405f4d: 48 c7 c1 fe ff ff ff mov rcx,0xfffffffffffffffe
405f54: eb 14 jmp 0x405f6a
405f56: 3c 08 cmp al,0x8
405f58: 75 30 jne 0x405f8a
405f5a: 48 c7 c3 fe ff ff ff mov rbx,0xfffffffffffffffe
405f61: 48 c7 c1 ff ff ff ff mov rcx,0xffffffffffffffff
405f68: eb 00 jmp 0x405f6a
405f6a: 48 6b db 0c imul rbx,rbx,0xc
405f6e: 48 01 cb add rbx,rcx
405f71: 48 69 db cd 00 00 00 imul rbx,rbx,0xcd
405f78: 48 8d 05 f9 ff ff ff lea rax,[rip+0xfffffffffffffff9] # 0x405f78
405f7f: 48 2d ba 00 00 00 sub rax,0xba
405f85: 48 01 d8 add rax,rbx
405f88: ff e0 jmp rax
405f8a: c3 ret
Fortunately, objdump is kinda enough to highlight these addresses (and only these addresses!). So it's pretty straightforward to clean this up a bit.
objdump -D -Mintel ./maze_public | rg -v nop | tail -n +67 | head -n -77 | rg "# " | rg ".*?# (.*)" -r '$1'
0x4015df
0x401699
0x4016ac
0x401766
0x401779
...
Each pair of addresses represent (node, base successor address) and everything else is static so can be computed.
import networkx as nx
def chunks(lst, n):
"""Yield successive n-sized chunks from lst."""
for i in range(0, len(lst), n):
yield lst[i:i + n]
with open("functions.txt","r") as f:
lines = [x.rstrip() for x in f.readlines()]
G = nx.DiGraph()
labels = {}
for a,b in chunks(lines, 2):
G.add_node(a)
for a,b in chunks(lines, 2):
def compute(base, rbx, rcx):
return (rcx + rbx * 0xc)*0xcd + (int(base,16) - 0xba)
for tag, rbx, rcx in [("1", -2, 1), ("2",-1,2), ("3", 1, 2), ("4", 2, 1), ("5", 2, -1), ("6", 1, -2), ("7", -1, -2), ("8", -2,-1)]:
next_node = hex(compute(b, rbx, rcx))
labels[(a,next_node)] = tag
G.add_edge(a,next_node)
# construct adjacency list and prune terminal nodes
adj = {k: [x for x in G.neighbors(k) if len(list(G.neighbors(x))) > 0] for k in G.nodes}
adj = {k: v for k, v in adj.items() if len(v) > 0}
mapping = {"0x403eb6": 0} # this is our start node so instead of modifying the cpp im just gonna make 0 the first node
count = 1
for i in adj.keys():
if i == "0x403eb6":
continue
mapping[i] = count
count += 1
print(f"{len(adj.keys())} {sum([len(x) for x in adj.values()])}")
for k,v in adj.items():
for i in v:
print(f"{mapping[k]} {mapping[i]}")
solving for the hamiltonian path
Now begins the long long search for a heuristic solution which does not segfault and will solve the problem in a reasonable time!
I ended up using a github repository mraggi/LongestSimplePath with some minor modifications to only find paths starting with node 0 and to take a graph from stdin.
❯ python make_graph.py | ~/Downloads/LongestSimplePath/lsp
Created graph!
Digraph on 64 vertices: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 ]
Finished preprocessing in: 0.093459
Doing DFS search...
Found DFS improvement at 8.5e-05 to 63
Done DFS search! Best Value = 63
Time taken for dfs: 0.900292
Doing PTO improving search...
The best path I found for graph G with the default options has value 63
0 50 56 41 58 48 34 17 2 12 6 16 31 47 62 52 46 63 53 59 49 33 18 1 11 5 15 32 22 7 24 14 8 23 39 54 60 45 55 61 51 57 40 26 9 3 13 19 4 10 25 35 20 30 44 38 29 43 27 21 37 28 42 36
Woohoo! A path! At this point all that is left is to translate it back into ascii numbers
import networkx as nx
from collections import deque
def window(seq, n=2):
it = iter(seq)
win = deque((next(it, None) for _ in range(n)), maxlen=n)
yield win
append = win.append
for e in it:
append(e)
yield win
def chunks(lst, n):
"""Yield successive n-sized chunks from lst."""
for i in range(0, len(lst), n):
yield lst[i:i + n]
with open("functions.txt","r") as f:
lines = [x.rstrip() for x in f.readlines()]
G = nx.DiGraph()
labels = {}
for a,b in chunks(lines, 2):
G.add_node(a)
for a,b in chunks(lines, 2):
def compute(base, rbx, rcx):
return (rcx + rbx * 0xc)*0xcd + (int(base,16) - 0xba)
for tag, rbx, rcx in [("1", -2, 1), ("2",-1,2), ("3", 1, 2), ("4", 2, 1), ("5", 2, -1), ("6", 1, -2), ("7", -1, -2), ("8", -2,-1)]:
next_node = hex(compute(b, rbx, rcx))
labels[(a,next_node)] = tag
G.add_edge(a,next_node)
adj = {k: [x for x in G.neighbors(k) if len(list(G.neighbors(x))) > 0] for k in G.nodes}
adj = {k: v for k, v in adj.items() if len(v) > 0}
mapping = {"0x403eb6": 0}
count = 1
for i in adj.keys():
if i == "0x403eb6":
continue
mapping[i] = count
count += 1
reverse_mapping = {v:k for k,v in mapping.items()}
cycle = [int(x) for x in "0 50 56 41 58 48 34 17 2 12 6 16 31 47 62 52 46 63 53 59 49 33 18 1 11 5 15 32 22 7 24 14 8 23 39 54 60 45 55 61 51 57 40 26 9 3 13 19 4 10 25 35 20 30 44 38 29 43 27 21 37 28 42 36".split(" ")]
for i in window(cycle):
print(labels[(reverse_mapping[i[0]],reverse_mapping[i[1]])],end="")
❯ python path_to_input.py
561471813235457247678183234714725456136768182361653135275824752% ❯ ./maze_public
Please type your input:
561471813235457247678183234714725456136768182361653135275824752
Well done! Please validate the input on the remote server
And that's it!
flag: flag{Kn1ght_t0ur_0n_chess_b0ard}